Introducción
$\DeclareMathOperator{\diag}{diag}$
En el año de 1985 el cosmonauta Vladimir Dzhanibekov, a bordo del módulo espacial Soyuz T-13 de la Unión Soviética, observó el comportamiento extraño de una tuerca de mariposa que giraba en gravedad cero.
La tuerca giraba sobre uno de sus ejes y periódicamente cambiaba de orientación sin la presencia de ninguna fuerza exterior.
Este comportamiento 1Muller, Derek. n.d. “The Bizarre Behavior of Rotating Bodies, Explained.” https://www.youtube.com/watch?v=1VPfZ_XzisU., una consecuencia del teorema del eje intermedio , recibió el nombre de Efecto de Dzhanibekov y es el tema de este artículo.
Se utilizará un enfoque basado en la mecánica clásica centrado en el análisis de cuerpos rígidos en movimiento para modelar 2Tao, Terrence. n.d. “The ‘Dzhanibekov Effect’ – an Exercise in Mechanics or Fiction? Explain Mathematically a Video from a Space Station.” https://mathoverflow.net/questions/81960/the-dzhanibekov-effect-an-exercise-in-mechanics-or-fiction-explain-mathemat. y explicar el extraño comportamiento de la tuerca de Dzhanibekov.
Por la naturaleza del problema y para comprender el modelo que se esta planteando es necesario utilizar varios conceptos de la mecánica clásica, por lo que se comenzará definiendo algunos de los conceptos que serán necesarios para poder plantear una serie de ecuaciones que describan el movimiento de la tuerca.
Nociones preliminares
En la física se hace un énfasis importante en el sistema de coordenadas con el que se esta trabajando con el objetivo de poder atribuir a cada objeto que se estudia una posición en el espacio.
Dentro del contexto de este artículo se tomará como una representación sensata del espacio en el que nos hallamos el espacio euclidiano $\mathbb{R}^{3}$ generado por una base ortogonal $\mathcal{X} = \left\{x,y,z\right\}$.
Se introduce de esta forma la siguiente definición:
Definición [Marco de referencia inercial]:
En la física clásica un marco de referencia inercial es un sistema de coordenadas $\mathcal{X}$ en el que para todo objeto, siempre que la suma de las fuerzas que actúan sobre el sea cero, este no está sujeto a ninguna aceleración. 3Taylor, John R. 2005. Classical Mechanics. University Science Books.
Trabajaremos con el supuesto apropiado de que nuestro marco de referencia $\mathcal{X}$ es inercial.
El estudio de objetos en rotación requiere la definición de las nociones de momento y velocidad angular.
Cursos introductorios de física tratan estos conceptos para un punto masa $p$ de masa $m$ y posición en el espacio $\boldsymbol{r}$.
Sin embargo, el estudio práctico de un cuerpo en rotación trata con objetos que tienen volumen y por lo tanto no pueden ser representados como un punto-masa.
Un análisis ligeramente más complejo, pero con mayor fidelidad a la realidad, requiere contemplar un objeto de manera que en lugar de considerar un punto masa consideramos una agrupación de puntos-masa en una región del espacio.
Esto motiva las siguientes definiciones:
Definición [Cuerpo Rígido]:
Un cuerpo rígido es una colección de N partículas con la propiedad de que la distancia entre ellas no cambia. 4Vladimir, Arnold, I. 1989. Mathematical Methods of Classical Mechanics Graduate Texts in Mathematics, 60. Graduate Texts in Mathematics. Springer-Verlag, New York.
Definición [Centro de Masa]:
El centro de masa de $N$ partículas, donde $ \textbf{r}_{\alpha} $ y $ \;m_{\alpha} $ representan la posición y peso de la $ \alpha $-ésima partícula respectivamente, es la posición dada por
$$ \boldsymbol{R} = \frac{1}{\overline{m}}\sum_{\alpha = 1}^{N} \boldsymbol{r}_{\alpha}m_{\alpha} $$
donde $\overline{m}$ denota el peso total de las $N$ partículas.5Taylor, John R. 2005. Classical Mechanics. University Science Books.
No es complicado mostrar que bajo el supuesto de que se trata con un cuerpo rígido, el centro de masa de este se comporta como un punto-masa de masa $\overline{m}$, facilitando en gran medida nuestro análisis.
Una demostración del hecho puede ser encontrada en 6Taylor, John R. 2005. Classical Mechanics. University Science Books..
Podemos así hablar del momento angular y velocidad angular de un cuerpo rígido al hablar del momento angular y velocidad angular de su centro de masa.
Definición [Momento Angular]:
Dado un sólido rígido de N partículas donde $\boldsymbol{r}_{\alpha}$ denota la posición de una partícula respecto al centro de masa; $m_{\alpha}$ denota su masa y $\boldsymbol{\omega}$ denota la velocidad angular del solido, el momento angular se define como:
$$ L := \sum\left\{ m_{\alpha}\boldsymbol{r}_{\alpha}\times\left(\boldsymbol{\omega}\times\boldsymbol{r}_{\alpha}\right)\right\}, $$
donde $\times$ es la relación binaria del producto cruz vectorial.
Definición [Momento de Inercia sobre el eje de rotación $z$]:
Dado un marco de referencia $\mathcal{X} = \left\{x,y,z\right\}$, el momento de inercia sobre el eje de rotación z, denotado por $I_{zz}$, se define como:
$$ I_{zz} = \sum_{\alpha}m_{\alpha}\delta^{2}_{\alpha}\;\;\;\delta^{2}_{\alpha}:= (x^{2}_{\alpha}+y^{2}_{\alpha}). $$
Los Momentos de Inercia sobre el eje de rotación $x,y$ se definen de forma análoga.
Observación:
$\delta_{\alpha}^{2}$ corresponde a la distancia del punto-masa del eje $z$ en este caso.
Definición [Producto de inercia del eje $x$ respecto a $z$]:
Se denota al producto de inercia del eje $x$ respecto a $z$ por $I_{xz}$ y se define como:
$$ I_{xz}:= -\sum_{\alpha}m_{\alpha}x_{\alpha}z_{\alpha}. $$
El resto de los productos de inercia se definen de manera análoga.
Observación:
Por definición, $I_{xz} = I_{zx}$.
Definición [Torque]:
El torque $\Gamma$ que actúa sobre una partícula determina el cambio en el momento angular respecto al tiempo:
$$ \Gamma = \frac{dL}{dt}. $$
El momento angular de un sólido en rotación
Enunciamos el siguiente teorema obtenido de 7Vladimir, Arnold, I. 1989. Mathematical Methods of Classical Mechanics Graduate Texts in Mathematics, 60. Graduate Texts in Mathematics. Springer-Verlag, New York..
Teorema [Momento angular de un cuerpo rígido respecto a su centro de masa]:
El momento angular $\textbf{L}$ de un cuerpo rígido con respecto al origen $\mathcal{O}$ depende linealmente del vector de velocidad angular $\;\boldsymbol{\Omega}$.
Es decir, existe un operador simétrico
$\textbf{A}$ tal que $\textbf{L}$ = $\textbf{A}\boldsymbol{\Omega}$.
Sea $\boldsymbol{\omega} = \left(\omega_{x},\omega_{y},\omega_{z}\right)$ la velocidad angular de un solido en rotación y $\boldsymbol{r}_{\alpha} = \left(x_{\alpha},y_{\alpha},z_{\alpha}\right)$ la posición de cada partícula respecto al centro de masa $\textbf{R}$, el cual podemos tomar como el origen $\mathcal{O}$ del sistema de coordenadas.
Consideremos la definición de Momento Angular y observemos que:
\[
m_{\alpha}\boldsymbol{r}_{\alpha}\times(\boldsymbol{\omega}\times\boldsymbol{r}_{\alpha}) = m_{\alpha} \left( \boldsymbol{r}_{\alpha}\times(\boldsymbol{\omega}\times\boldsymbol{r}_{\alpha})\right) = m_{\alpha}
\begin{bmatrix}
(y_{\alpha}^{2}+z_{\alpha}^{2})\omega_{x} -x_{\alpha}y_{\alpha}\omega_{y}-x_{\alpha}z_{\alpha}\omega_{z}\\
-y_{\alpha}x_{\alpha}\omega_{x}+(z_{\alpha}^{2}+x_{\alpha}^{2})\omega_{y}-y_{\alpha}z_{\alpha}\omega_{z}\\
-z_{\alpha}x_{\alpha}\omega_{x}-z_{\alpha}y_{\alpha}\omega_{y}+(x_{\alpha}^{2}+y_{\alpha}^{2})\omega_{z}\\
\end{bmatrix}.
\]
Al sumar sobre $\alpha$ y utilizar las definiciones de Momento Angular, Momento de Inercia y Producto de Inercia, encontramos el momento angular de un cuerpo rígido que esta girando sobre cualquier eje:
\begin{equation}
\tag{L_tensorial}
\boldsymbol{L} =
\begin{bmatrix}
I_{xx}&I_{xy}&I_{xz} \\
I_{yx}&I_{yy}&I_{yz}\\
I_{zx}&I_{zy}&I{zz}
\end{bmatrix}
\begin{bmatrix}
\omega_{x} \\
\omega_{y} \\
\omega_{z}
\end{bmatrix}.
\end{equation}
$$
La matriz de $3 \times 3$ en [L_tensorial] se conoce como el tensor de inercia .
Notemos ahora que el vector de momento angular respecto al centro de masa del sólido, denotado por $\boldsymbol{L}$, siempre puede ser expresado respecto al marco de referencia estático por medio de una matriz de cambio de base $\textbf{B}$ tal que $\boldsymbol{l} = \boldsymbol{B}\boldsymbol{L}$.
Sin embargo, sabemos que el momento angular en una marco de referencia inercial se conserva, de tal forma que se cumple que $\boldsymbol{l} = \textbf{B}_{t}\boldsymbol{L}(t)$.
Si tomamos la derivada respecto al tiempo de esta ecuación tenemos que:
$$ \dot{\boldsymbol{l}}= \frac{d}{dt}\boldsymbol{BL} = \boldsymbol{B}\dot{\boldsymbol{L}} + \boldsymbol{\omega}\times\boldsymbol{l} = \boldsymbol{B}(\dot{\boldsymbol{L}} + \boldsymbol{B}^{-1}(\boldsymbol{\omega}\times \boldsymbol{l})) = \boldsymbol{B}(\dot{\boldsymbol{L}} + \boldsymbol{\Omega}\times \boldsymbol{L}). $$
Pero como hemos visto que el momento angular en el marco de referencia inercial se conserva, tenemos que $\textbf{l}$ es constante y $\dot{\textbf{l}} = 0$.
Por lo tanto llegamos a la importante relación:
\tag{Ecuacion de Euler}
\dot{\boldsymbol{L}} = \boldsymbol{L}\times\boldsymbol{\Omega}.
\end{equation}
Esta relación es conocida como las ecuaciones de Euler homogéneas, pues el hecho de que el momento angular sea constante es una consecuencia directa de tomar como supuesto que la fuerzas que actúan sobre el objeto respecto a $\mathcal{O}$ son nulas.
De acuerdo a la definición [Torque] esto quiere decir que el torque es nulo.
Análisis y planteamiento del problema
Ecuaciones de Euler
En la mecánica clásica, las ecuaciones de Euler describen el movimiento de un sólido rígido en rotación.
Recordando la ecuación [L_tensorial] cabe destacar dos cosas:
En primer lugar, podemos escribir las ecuaciones de Euler de la forma
$$ \dot{\boldsymbol{L}} = (\boldsymbol{I}\boldsymbol{\Omega})\times\boldsymbol{\Omega}. $$
Observación:
En el contexto de este problema, recordemos que $\boldsymbol{I}$ corresponde al tensor de inercia, no a la matriz identidad.
En segundo lugar, cuando se gira sobre un eje arbitrario, frecuentemente será el caso que el vector de momento angular no sea paralelo al vector de velocidad angular.
El caso especial en el que $\boldsymbol{L} = k\boldsymbol{\Omega}$ para alguna constante $k$ se da solo cuando el tensor de inercia es una matriz diagonal, es decir, cuando los productos de inercia respecto a cada eje son nulos.
Hacemos la observación de que una vez que el tensor de inercia es una matriz simétrica, sus eigenvectores forman una base ortogonal para el espacio $\mathbb{R}^{3}$.
Esto motiva la siguiente definición:
Definición [Ejes Principales]:
Sea $\mathcal{S}$ un sólido rígido.
Las direcciones características del tensor de inercia son los ejes principales del sólido $\mathcal{S}$.
Observación:
En el caso particular de que $\mathcal{S}$ este girando sobre su eje principal, tenemos que $L_{i} = I_{i} \boldsymbol{\Omega}_{i}$, donde $I_{i}$ representa al $i$-ésimo elemento de la diagonal del tensor de inercia $\boldsymbol{I}$.
Por lo tanto, se justifica el hacer nuestro análisis en un marco de referencia no inercial que va rotando en el tiempo al caracterizar a este marco de referencia con el sistema de coordenadas centrado en $\mathcal{O}$, $\boldsymbol{\chi} = \{ e_{1},e_{2},e_{3}\}$, el cual corresponde a las direcciones propias del tensor de inercia en cada momento.
De esta forma, la ecuación [Ecuación de Euler] se puede escribir de la siguiente manera:
\begin{cases}
I_{1}\dot{\Omega}_{1}+\left(I_{3}-I_{2}\right)\Omega_{2}\Omega_{3} =0 & \\
I_{2}\dot{\Omega}_{2}+\left(I_{1}-I_{3}\right)\Omega_{3}\Omega_{1} =0 & \\
I_{3}\dot{\Omega}_{3}+\left(I_{2}-I_{1}\right)\Omega_{1}\Omega_{2} =0 & .
\end{cases}
\end{equation}
Ahora bien, sea $\mathcal{S}$ un sólido rígido con momentos de inercia $I_{1},I_{2},I_{3}$ tales que $I_{1} \neq I_{2} \neq I_{3} \neq 0 $.
Denotamos por $\boldsymbol{\Omega} = (\Omega_{1},\Omega_{2},\Omega_{3})$ el vector de velocidad angular de $\mathcal{S}$ respecto a su centro de masa.
El sistema [Eq.Euler Homogeneo] tiene 4 puntos de equilibrio:
\begin{equation*}
\begin{cases}
\boldsymbol{\Omega}_{\star} = (0,0,0) \\
\boldsymbol{\Omega}_{\star} = (\alpha,0,0) \\
\boldsymbol{\Omega}_{\star} = (0,\alpha,0) \\
\boldsymbol{\Omega}_{\star} = (0,0,\alpha).
\end{cases}
\end{equation*}
Por la definición de punto de equilibrio, es aparente que si el sólido tiene una velocidad angular inicial de alguna de estas formas, la velocidad angular no cambiará.
En este momento vale la pena recordar que la velocidad angular no es un escalar; tiene una dirección y magnitud al ser una cantidad vectorial.
La ventaja de haber definido un sistema de coordenadas ortogonal a partir del centro de masa del sólido radica en que la descomposición del vector de velocidad angular en componentes coincide en ser la descomposición de la velocidad angular sobre cada uno de sus 3 ejes principales.
Teniendo esto en mente es fácil caer en cuenta de que si la condición inicial es de la forma de alguno de lo puntos de equilibrio no nulos, entonces la velocidad angular será constante en magnitud y dirección.
El converso es verdadero también 8Taylor, John R. 2005. Classical Mechanics. University Science Books..
Esto se aprecia trivialmente de la forma que toma el sistema [Eq.Euler Homogeneo] ante condiciones iniciales de la forma de los puntos de equilibrio:
las velocidades angulares son funciones constantes ante el tiempo y por lo mismo toman el valor de la condición inicial.
Es decir, si el objeto comienza girando a cierta magnitud en una dirección canónica, se mantendrá así siempre y cuando no actúen sobre él fuerzas externas.
Ahora consideremos el caso de la condición inicial $\boldsymbol{\Omega} = (\alpha,\varepsilon_{2},\varepsilon_{3})$, con $\varepsilon_{i}$ muy pequeño.
De las ecuaciones de Euler obtenemos el sistema:
\begin{cases}
\dot{\Omega}_{1} = \left(\frac{I_{2}-I_{3}}{I_{1}}\right)\Omega_{2}\Omega_{3}\\ \\
\dot{\Omega}_{2} = \left(\frac{I_{3}-I_{1}}{I_{2}}\right)\Omega_{3}\Omega_{1}\\ \\
\dot{\Omega}_{3} = \left(\frac{I_{1}-I_{2}}{I_{3}}\right)\Omega_{1}\Omega_{2}.
\end{cases}
\end{equation}
En el caso que $\varepsilon_{2}$ y $\varepsilon_{3}$ son de magnitud muy pequeña, como lo hemos supuesto, se cumple que el producto $\varepsilon_{2}\varepsilon_{3}$ lo es aun más.
Por lo tanto tenemos que $\dot{\Omega}_{1} \approx 0$ y tomar $\Omega_{1} = K$ con $K$ una constante es una aproximación razonable 9Palaniappan, Vivek. n.d. “Tennis Racket Theorem.” https://medium.com/engineer-quant/tennis-racket-theorem-8fb391098e34..
Haciendo esto, el sistema [Eq.Euler W1 con perturbacion] se reduce a lo siguiente:
\begin{cases}
\dot{\Omega}_{2} = \left(\frac{I_{3}-I_{1}}{I_{2}}\right)K\Omega_{3}\\ \\
\dot{\Omega}_{3} = \left(\frac{I_{1}-I_{2}}{I_{3}}\right)K\Omega_{2}
\end{cases}
\implies
\begin{cases}
\dot{\Omega}_{2} = \rho_{2}\Omega_{3} \\
\dot{\Omega}_{3} = \rho_{3}\Omega_{2}
\end{cases}
\end{equation}
Se deben apreciar algunos hechos sobre el sistema [Eq.Euler W1 con perturbacion reducido].
En primer lugar, estamos lidiando con un sistema lineal.
Por otra parte, si tomamos como supuesto un orden sobre los momentos de inercia anteriormente definidos tal que $I_{1} < I_{2} < I_{3}$, entonces es fácil comprobar que las constantes $\rho_{1}$ y $\rho_{2}$ tienen signo opuesto.
Teniendo esto en mente volvemos a replantear nuestro sistema, ahora de forma matricial:
\begin{bmatrix}
\dot{\Omega}_{2}\\
\dot{\Omega}_{3}\\
\end{bmatrix}
=
\begin{bmatrix}
0 & \rho_{2}\\
\rho_{3} & 0\\
\end{bmatrix}
\begin{bmatrix}
\Omega_{2} \\
\Omega_{3}
\end{bmatrix}.
\end{equation}
De la observación que hicimos respecto a los signos de $\rho_{2}$ y $\rho_{2}$ se vuelve aparente que el [Sistema Matricial Complejo] tiene dos eigenvalores complejos con parte real nula.
Claramente estos eigenvalores $\lambda_{1},\lambda_{2}$ son conjugados al igual que sus eigenvectores.
Es fácil verificar que el eigenpar $(\lambda_{1},W_{1})$ esta dado por:
\[
\lambda_{1} = i\sqrt{-\rho_{2}\rho_{3}}\;,\quad \textbf{w}_{1} = \textbf{u}_{1}+i \textbf{v}_{1} =
\begin{bmatrix}
\rho_{2} \\
0
\end{bmatrix}
+ i
\begin{bmatrix}
0 \\
\sqrt{-\rho_{2}\rho_{3}}
\end{bmatrix}.
\]
Una vez que los valores propios son puramente imaginarios es evidente que $\lambda_{2} = \overline{\lambda}_{1} = -\lambda_{1}$ y así:
\[
\lambda_{2} = -i\sqrt{-\rho_{2}\rho_{3}}\;, \quad
\overline{\textbf{w}}_{1} = \textbf{u}_{1}-i \textbf{v}_{1} =
\begin{bmatrix}
\rho_{2} \\
0
\end{bmatrix}
-i
\begin{bmatrix}
0 \\
\sqrt{-\rho_{2}\rho_{3}}
\end{bmatrix}
\]
corresponde al otro eigenpar del sistema.
A continuación enunciamos y utilizamos el siguiente teorema y corolario de 10Perko, Lawrence. 2013. Differential Equations and Dynamical Systems. Vol. 7. Texts in Applied Mathematics. Springer.
Teorema [Eigenvalores complejos]:
Si una matriz real, $A$, de $2n\times2n$ tiene $2n$ eigenvalores distintos $\lambda_{j} = a_{j} + ib_{j}$ y $\overline{\lambda_{j}} = a_{j} – ib_{j}$ con los eigenvectores complejos correspondientes
$$ \textbf{w}_{j} = \textbf{u}_{j} + i\textbf{v}_{j} \text{ y } \overline{\textbf{w}_{j}} = \textbf{u}_{j} – i\textbf{v}_{j}, \quad j = 1,\dots,n $$
entonces $\{u_{1},v_{1},\dots,u_{n},v_{n} \}$ es una base para $\mathbb{R}^{2n}$.
La matriz $P = [u_{1} \, v_{1} \, \cdots \, u_{n} \, v_{n}]$ es invertible y
$P^{-1}AP = \diag
\begin{bmatrix}
a_{j} & -b_{j}\\
b_{j} & a_{j}\\
\end{bmatrix} $ es una matriz real de $2n\times2n$ con bloques de $2\times2$ a lo largo de la diagonal.
Corolario
Bajo la hipótesis del teorema anterior, la solución para el Problema de valor inicial (PVI)
\begin{align*}
\dot{x} &= Ax \\
x(0) &= x_{0}
\end{align*}
esta dada por
\[
x(t) = P\diag e^{a_{j}t}
\begin{bmatrix}
\cos{(b_{j}t)} & -\sin{(b_{j}t)}\\
\sin{(b_{j}t)} & \phantom{-}\cos{(b_{j}t)}
\end{bmatrix}
P^{-1}x_{0}.
\]
Por lo tanto, la solución al [Sistema Matricial Complejo] es:
\begin{equation*}
\boldsymbol{\Omega}(t) =
\begin{bmatrix}
0 & \rho_{2} \\
\sqrt{-\rho_{2}\rho_{3}} & 0
\end{bmatrix}
\begin{bmatrix}
\cos{\left(\sqrt{-\rho_{2}\rho_{3}}t\right)} & -\sin{\left(\sqrt{-\rho_{2}\rho_{3}}t\right)}\\ \
\sin{\left(\sqrt{-\rho_{2}\rho_{3}}t\right)} & \phantom{-}\cos{\left(\sqrt{-\rho_{2}\rho_{3}}t\right)}
\end{bmatrix}
\begin{bmatrix}
0 & \frac{1}{\sqrt{-\rho_{2}\rho_{3}}} \\
\frac{1}{\rho_{2}}& 0
\end{bmatrix}
\begin{bmatrix}
\varepsilon_{2} \\
\varepsilon_{3} .
\end{bmatrix}
\end{equation*}
Simplificando obtenemos la solución al sistema [Eq.Euler W1 con perturbacion]:
\begin{equation}
\begin{cases}
\Omega_{1} = \alpha \\ \\
\Omega_{2} = \varepsilon_{2}\cos{\left(\sqrt{-\rho_{2}\rho_{3}}t\right)} +\varepsilon_{3}\frac{\rho_{2}}{\sqrt{-\rho_{2}\rho_{3}}}\sin{\left(\sqrt{-\rho_{2}\rho_{3}}t\right)} \\ \\
\Omega_{3} = -\varepsilon_{2}\frac{\sqrt{-\rho_{2}\rho_{3}}}{\rho_{2}}\sin{\left(\sqrt{-\rho_{2}\rho_{3}}t\right)} + \varepsilon_{3}\cos{\left(\sqrt{-\rho_{2}\rho_{3}}t\right)}.
\end{cases}
\end{equation}
Si nos mantenemos sujetos a la hipótesis de que los momentos de inercia sobre cada eje son distintos y ordenados como
$I_{1} < I_{2} < I_{3}$ , el procedimiento para encontrar las soluciones analíticas del caso cuando la condición inicial es de la forma $\boldsymbol{\Omega} = (\varepsilon_{1},\varepsilon_{2},\alpha)$ es prácticamente el mismo.
Tendremos un sistema análogo a [Eq.Euler W1 con perturbacion], excepto que en esta situación tendremos que
\begin{equation*}
\begin{cases}
\dot{\Omega}_{1} = \left(\frac{I_{2}-I_{3}}{I_{1}}\right)K\Omega_{2}\\ \\
\dot{\Omega}_{2} = \left(\frac{I_{3}-I_{1}}{I_{2}}\right)K\Omega_{1}
\end{cases}
\implies
\begin{cases}
\dot{\Omega}_{1} = \rho_{1}\Omega_{2} \\
\dot{\Omega}_{2} = \rho_{2}\Omega_{1} .
\end{cases}
\end{equation*}
De nuevo podemos apreciar que los signos de las constantes, ahora $\rho_{1}$ y $\rho_{2}$, son opuestos.
Se sigue que tendremos la solución:
\begin{equation*}
\begin{cases}
\Omega_{1} = -\varepsilon_{2}\frac{\sqrt{-\rho_{2}\rho_{1}}}{\rho_{2}}\sin{\left(\sqrt{-\rho_{2}\rho_{1}}t\right)} + \varepsilon_{1}\cos{\left(\sqrt{-\rho_{2}\rho_{1}}t\right)}.\\ \\
\Omega_{2} = \varepsilon_{2}\cos{\left(\sqrt{-\rho_{2}\rho_{1}}t\right)} + \varepsilon_{1}\frac{\rho_{2}}{\sqrt{-\rho_{2}\rho_{1}}}\sin{\left(\sqrt{-\rho_{2}\rho_{1}}t\right)}\\\\
\Omega_{3} = \alpha.
\end{cases}
\end{equation*}
Resulta interesante llevar a cabo un análisis sobre la magnitud de la oscilación sobre los ejes principales con mayor y menor momento de inercia.
Ya que la forma de las soluciones para condiciones iniciales de la forma $\boldsymbol{\Omega} = (\alpha, \varepsilon_{2}, \varepsilon_{3})$ es análoga a condiciones iniciales de la forma $\boldsymbol{\Omega} = (\varepsilon_{1}, \varepsilon_{2}, \alpha)$, sin pérdida de generalidad, nos limitamos a analizar el primer caso.
\begin{align*}
\left| \Omega_{2} \right| & = \left| \varepsilon_{2}\cos{\left(\sqrt{-\rho_{2}\rho_{3}}t\right)} + \varepsilon_{3}\frac{\rho_{2}}{\sqrt{-\rho_{2}\rho_{3}}}\sin{\left(\sqrt{-\rho_{2}\rho_{3}}t\right)} \right|\\
& \leq \left| \varepsilon_{2}\cos{\left(\sqrt{-\rho_{2}\rho_{3}}t\right)} \right| + \left| \varepsilon_{3}\frac{\rho_{2}}{\sqrt{-\rho_{2}\rho_{3}}}\sin{\left(\sqrt{-\rho_{2}\rho_{3}}t\right)} \right| \\
& \leq \left| \varepsilon_{2} \right| + \left| \varepsilon_{3}\frac{\rho_{2}}{\sqrt{-\rho_{2}\rho_{3}}} \right| ,
\end{align*}
mientras que para $\Omega_{3}$ tenemos que:
\begin{align*}
\left| \Omega_{3} \right| & = \left| -\varepsilon_{2}\frac{\sqrt{-\rho_{2}\rho_{3}}}{\rho_{2}}\sin{\left(\sqrt{-\rho_{2}\rho_{3}}t\right)} + \varepsilon_{3}\cos{\left(\sqrt{-\rho_{2}\rho_{3}}t\right)} \right|\\
& \leq \left| -\varepsilon_{2}\frac{\sqrt{-\rho_{2}\rho_{3}}}{\rho_{2}}\sin{\left(\sqrt{-\rho_{2}\rho_{3}}t\right)} \right| + \left| \varepsilon_{3}\cos{\left(\sqrt{-\rho_{2}\rho_{3}}t\right)} \right|\\
& \leq \left| \varepsilon_{2}\frac{\sqrt{-\rho_{2}\rho_{3}}}{\rho_{2}} \right| + \left| \varepsilon_{3} \right| .
\end{align*}
Por ende, del análisis previo y de [Solucion sistema perturbado omega2] podemos concluir que una pequeña perturbación sobre el equilibrio $\boldsymbol{\Omega} = (\alpha, 0, 0)$ resulta en un crecimiento acotado de la perturbación.
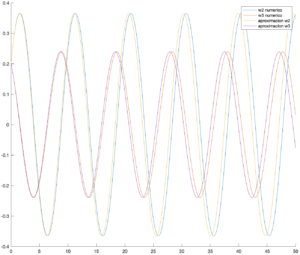
Se llevó a cabo un análisis numérico simple del comportamiento de las soluciones componente de $\boldsymbol{\Omega}$.
Se obtuvo la solución numérica a las ecuaciones de Euler con los siguientes valores:
$$ I_{1} = 2,\; I_{2} = 5,\;I_{3} = 7,\; \boldsymbol{\Omega}_{0} = (1,10^{-2},10^{-2}). $$
En el primer panel se aprecia el la gráfica de las soluciones componente, mientras que el segundo panel muestra la solución numérica obtenida y la aproximación que se dio en el análisis anterior para $\Omega_{1}$.
Se había mencionado que para perturbaciones pequeñas el tomar $\Omega_{1}$ como una constante era una aproximación razonable.
El tamaño de la oscilación de la solución numérica es más evidencia a favor de esta aseveración.
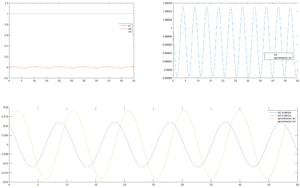
Por último, el panel inferior muestra con mayor detalle las oscilaciones de los otros dos componentes.
Para este caso el comportamiento numérico de las soluciones y el comportamiento que obtuvimos teóricamente a través de la aproximación inicial es tan buena que no se percibe gráficamente la diferencia.
Se requiere de una perturbación mucho más grande [en el orden de $0.2\alpha$ por ejemplo] para que se comience a ver una diferencia entre las soluciones analíticas aproximadas y las numéricas.
Mostramos esto en la siguiente figura:
Como se puede observar, el error causado por tomar como supuesto a $\Omega_{1}$ aproximadamente una constante va creciendo con el tiempo cuando la perturbación es de un tamaño relativamente grande comparado con la magnitud de $\alpha$.
Consideremos ahora una condición inicial de la forma $\boldsymbol{\Omega} = (\varepsilon_{1},\alpha,\varepsilon_{3})$, con $\varepsilon_{1}$ y $\varepsilon_{3}$ una vez más de magnitud muy pequeña.
Procedemos con un análisis cualitativamente idéntico al que hicimos para los casos anteriores con la excepción de que nos restringimos a una vecindad pequeña de la condición inicial donde tomamos $\dot{\Omega}_{2} \approx 0$.
Una vez mas, las ecuaciones de Euler se reducen localmente a algo de la forma:
\begin{cases}
\dot{\Omega}_{1} = \left(\frac{I_{2}-I_{3}}{I_{1}}\right)K\Omega_{3} \\ \\
\dot{\Omega}_{3} = \left(\frac{I_{1}-I_{2}}{I_{3}}\right)K\Omega_{1}
\end{cases}
\implies
\begin{cases}
\dot{\Omega}_{1} = \rho_{1}\Omega_{3} \\
\dot{\Omega}_{3} = \rho_{3}\Omega_{1}
\end{cases}
\end{equation}
Al igual que en el sistema [Eq.Euler W1 con perturbacion reducido], estamos lidiando con un sistema lineal.
Sin embargo, continuando con el supuesto de que existe un orden sobre los momentos de inercia tal que $I_{1} < I_{2} < I_{3}$, entonces es fácil comprobar que las constantes $\rho_{1},\rho_{3}$ tienen el mismo signo.
Teniendo esto en mente volvemos a replantear nuestro sistema de forma matricial:
\begin{bmatrix}
\dot{\Omega}_{1}\\
\dot{\Omega}_{3}
\end{bmatrix}
=
\begin{bmatrix}
0 & \rho_{1}\\
\rho_{3} & 0
\end{bmatrix}
\begin{bmatrix}
\Omega_{1} \\
\Omega_{3}
\end{bmatrix},
\end{equation}
de donde es evidente que [Sistema Matricial Exponencial] tiene dos eigenvalores reales con la misma magnitud, pero de signo contrario.
Es fácil verificar que los eigenpares $(\lambda_{1},w_{1}),$ $(\lambda_{2},w_{2})$ están dados por:
\begin{align*}
\lambda_{1} = \sqrt{\rho_{1}\rho_{3}}\;, \quad \textbf{w}_{1}
&=
\begin{bmatrix}
\rho_{1} \\
\sqrt{\rho_{1}\rho_{3}}
\end{bmatrix}
\\
\lambda_{2} = -\sqrt{\rho_{1}\rho_{3}}\;, \quad \textbf{w}_{2}
&=
\begin{bmatrix}
\rho_{1} \\
-\sqrt{\rho_{1}\rho_{3}}
\end{bmatrix}.
\end{align*}
A continuación enunciamos y utilizamos los siguiente resultados de 11Perko, Lawrence. 2013. Differential Equations and Dynamical Systems. Vol. 7. Texts in Applied Mathematics. Springer..
Teorema [Fundamental de los Sistemas Lineares]:
Si una matriz real, A, de $n\times n.$ Entonces para un dado $x_{0}\in\mathbb{R}$, el Problema de valor inicial (PVI)
\begin{align*}
\dot{x} &= Ax \\
x(0) &= x_{0}
\end{align*}
tiene una solución única y esta dada por
$x(t) = e^{At}x_{0}$
Proposición [Matriz Exponencial]:
Sean $P$ y $S$ transformaciones lineales en $\mathbb{R}^n$ y tales que $A=PSP^{-1}$, entonces
$$ e^{A} = Pe^SP^{-1} . $$
Corolario
Si $P^{-1}AP=S= \diag \left(\lambda_{j} \right)$, entonces
\begin{equation}
e^{At} = P\diag \left( e^{\lambda_{j}t} \right) P^{-1} .
\end{equation}
Por lo tanto, la solución al [Sistema Matricial Exponencial] es:
\begin{equation*}
\boldsymbol{\Omega}(t) =
\begin{bmatrix}
\rho_{1} & \rho_{1} \\
\sqrt{\rho_{1}\rho_{3}} & -\sqrt{\rho_{1}\rho_{3}}
\end{bmatrix}
\begin{bmatrix}
e^{\sqrt{\rho_{1}\rho_{3}}t} & 0 \\
0 & e^{-\sqrt{\rho_{1}\rho_{3}}t}
\end{bmatrix}
\begin{bmatrix}
\rho_{1} & \rho_{1} \\
\sqrt{\rho_{1}\rho_{3}} & -\sqrt{\rho_{1}\rho_{3}}
\end{bmatrix}^{-1}
\begin{bmatrix}
\varepsilon_{1} \\
\varepsilon_{3}
\end{bmatrix} .
\end{equation*}
Simplificando obtenemos una solución local aproximada al sistema [Eq.Euler W2 con perturbacion reducido]:
\begin{cases}
\Omega_{1} = \frac{\rho_{1}}{2}(\frac{\varepsilon{1}}{\rho_{1}}(e^{\sqrt{\rho_{1}\rho_{3}}t} + e^{-\sqrt{\rho_{1}\rho_{3}}t}) + \frac{\varepsilon{3}}{\sqrt{\rho_{1}\rho_{3}}}(e^{\sqrt{\rho_{1}\rho_{3}}t} – e^{-\sqrt{\rho_{1}\rho_{3}}t}))\\
\Omega_{2} = \alpha \\
\Omega_{3} = \frac{\sqrt{\rho_{1}\rho_{3}}}{2} (\frac{\varepsilon{1}}{\rho_{1}}(e^{\sqrt{\rho_{1}\rho_{3}}t} – e^{-\sqrt{\rho_{1}\rho_{3}}t}) – \frac{\varepsilon{3}}{\sqrt{\rho_{1}\rho_{3}}}(e^{\sqrt{\rho_{1}\rho_{3}}t} – e^{-\sqrt{\rho_{1}\rho_{3}}t}))
\end{cases}
\end{equation}
Observación:
Para una condición inicial de la forma $(0,\alpha,0)$, para un intervalo de tiempo finito el componente de velocidad angular $\Omega_{2}$ es localmente aproximado relativamente bien por una constante, mientras que las velocidades angulares en los otros dos componentes son combinaciones lineales de senos y cosenos hiperbólicos.
Dado [Solucion sistema perturbado omega2] podemos ver que incluso localmente las perturbación crecen de manera exponencial y que por lo tanto, las rotaciones alrededor del eje principal con el momento de inercia intermedio son muy sensibles a perturbaciones sobre los otros ejes principales.
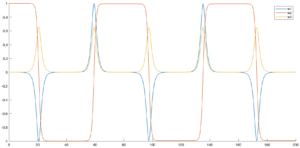
Las soluciones componente numéricas para este caso son visualmente llamativas.
Se llevó a cabo una solución numérica con los mismos valores para los momentos de inercia, utilizando perturbaciones considerablemente mas pequeñas, $e_{i} = 10^{-5}$.
En la figura [orbitas inestables] podemos observar el Efecto de Dhzanibekov.
En ausencia de fuerzas exteriores, [recordemos que por hipótesis, la suma de las fuerzas exteriores y por lo tanto el torque, son cero] se observa una alternancia en la dirección de $\Omega_{2}$ sujeta a la misma magnitud periódicamente, y el comportamiento de los otros componentes de velocidad angular parece ser periódico también.
Esta observación, en consideración con los resultados recabados anteriormente, sugiere una estructura familiar: Las curvas fase parecieran ser cerradas.
Para hacer un análisis de su estructura, recordemos que el momento angular $\boldsymbol{L}$ depende linealmente de la velocidad angular $\boldsymbol{\Omega}$.
Podemos, por ende, llevar a cabo un análisis de las curvas de fase análogamente planteando las ecuaciones de Euler como un sistema diferencial respecto a $\boldsymbol{L}$.
Para llevar a cabo este análisis enunciamos la siguiente definición que se puede encontrar en 12Arnold Vladimir, I. Ordinary Differential Equations. Universitext. Springer-Verlag, 1992.
Definición [Primera integral cuadrática]:
Sea v un campo vectorial e $\mathcal{I} \colon U \to \mathbb{R}$ una función diferenciable.
La función $\mathcal{I}$ se conoce como primera integral de una ecuación $\dot{x} = v(x)$ si $\nabla\mathcal{I}v(x) = 0$.
La función $\mathcal{I}$ es una primera integral cuadrática si $\mathcal{I}$ es una primera integral y si existe una matriz simétrica $C$ tal que $\mathcal{I} = x^{T}Cx$.
Las siguientes enunciados son formulaciones equivalentes:
- La primera integral $\mathcal{I}$ es constante a lo largo de soluciones al sistema.
- Cada curva fase pertenece a una y solo una curva de nivel de la función $\mathcal{I}$
Observación:
Una primera integral es una cantidad conservada y por lo tanto, una primera integral cuadrática también lo es.
Las ecuaciones de Euler para cuerpos rígidos admiten dos integrales cuadráticas de primer orden,
\begin{equation}
2E = \frac{{L_{1}}^2}{I_{1}} + \frac{{L_{2}}^2}{I_{2}} + \frac{{L_{3}}^2}{I_{3}} \text{ y } M^2 = {L_{1}}^2 +{L_{2}}^2 +{L_{3}}^2 ,
\end{equation}
donde $L_{i}$ es el momento angular respecto a algún eje.
Demostración
Para la primera integral, basta tomar $C = \diag \left( \frac{1}{I_{1}},\frac{1}{I_{2}},\frac{1}{I_{3}} \right)$ y para la segunda $C = \mathbb{I}$.
Se verifica que
$$ \nabla\mathcal{I}v(x) = 0 $$
al recordar que para las ecuaciones de Euler, en términos de $\boldsymbol{L}$ nos da que $\dot{\boldsymbol{L}} = \boldsymbol{L}\times\Omega$.$\square$
Las cantidades conservadas que hemos hallado son superficies de nivel.
Al tomar la intersección de estas tendremos las curvas que corresponden al flujo 13Vladimir, Arnold, I. 1989. Mathematical Methods of Classical Mechanics Graduate Texts in Mathematics, 60. Graduate Texts in Mathematics. Springer-Verlag, New York..
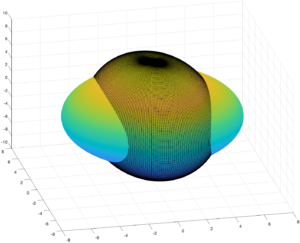
Por ende, las soluciones se encuentra en la intersección de un elipsoide con una esfera.
Bajo nuestro supuesto de que $I_{1} < I_{2} < I_{3}$, los semiejes del elipsoide serian $\sqrt{2EI_{1}} < \sqrt{2EI_{2}} < \sqrt{2EI_{3}}$.
Ahora, para $E$ fijo, hagamos variar el radio de la esfera $M$.
- Si $M < \sqrt{2EI_{1}}$ o si $\sqrt{2EI_{3}} < M$ entonces la intersección es el vacío y ningún movimiento existe para los valores de $E$ y $M$.
- Si $M = \sqrt{2EI_{1}}$ o si $\sqrt{2EI_{3}} = M$ entonces la intersección consiste de dos puntos únicamente en las orillas del semieje.
- Si $ \sqrt{2EI_{1}} < M < \sqrt{2EI_{3}}$ obtenemos dos curvas alrededor de las orillas del semieje más pequeño y del más grande.
- Si $M = \sqrt{2EI_{2}}$ la intersección consiste en dos círculos 14Vladimir, Arnold, I. 1989. Mathematical Methods of Classical Mechanics Graduate Texts in Mathematics, 60. Graduate Texts in Mathematics. Springer-Verlag, New York..
Para facilitar la visualización de la forma que tomaran las curvas, obsérvese la figura [3d figs].
Esta corresponde al las soluciones para niveles de energía fijos $E,M$ dados los momentos de inercia que hemos estado utilizando hasta ahora, $(I_{1} = 2,I_{2} = 5, I_{3} = 7 )$.
Al correr la simulación numérica para las ecuaciones de Euler respecto al momento angular, obtenemos una de las curvas cerrada correspondientes a esta intersección, la cual pueden ser observadas en la figura [Trayectorias en el espacio].
Conclusión
El estudio de los sólidos en rotación requiere de una cantidad de trabajo importante y de una base decente sobre lo que se esta tratando.
A lo largo del presente articulo se hizo aparente que todo el tiempo se estuvo trabajando con la versión equivalente (rotacional) de las Leyes de Newton, y que estas podían explicar completamente el extraño comportamiento de la tuerca que observó Dhzanibekov.
En efecto, la primera ley de Newton explícitamente dice que cualquier objeto al que no se le este aplicando una fuerza neta no nula permanecerá con velocidad constante al no acelerar.
Sabemos que los objetos en movimiento circular uniforme tienen una aceleración centrípeta que los mantiene en su trayectoria, pero ¿Cómo explicar el cambio tan radical de la tuerca?
Un cambio de dirección tan brusco sin la presencia de fuerzas exteriores parecería ir en contra de las leyes de Newton.
No es hasta que uno traduce las leyes de Newton al ámbito del movimiento circular uniforme y luego al reino de los marcos de referencia no inerciales que el movimiento periódico de la tuerca se explica dentro del marco de estas leyes.
Como se vio, resulta ser que bajo ciertas condiciones de las propiedades físicas del objeto en cuestión [la inercia de sus ejes principales] este tipo de movimiento es una consecuencia esperada.
En la literatura esto se conoce como el teorema del eje intermedio, o como el teorema de la raqueta de tenis.
Vimos que al traducir las Leyes de Newton a un marco de referencia no inercial se obtienen las ecuaciones de Euler, las cuales al ser vistas como una ecuación diferencial ordinaria nos proporcionan una manera de describir exhaustivamente el movimiento de una partícula del sólido.
Ya que las partículas de un cuerpo rígido mantienen la distancia entre si, podemos describir el movimiento de la tuerca, o algún otro cuerpo rígido con tres momentos de inercia distintos.
Si bien la solución de las ecuaciones de Euler es la velocidad angular o el momento angular, dependiendo de que enfoque se tome, de estos parámetros podemos describir la posición en el espacio de cualquier partícula del objeto.
En efecto, la relación entre momento angular y velocidad angular es lineal, y la relación entre la velocidad en el espacio y velocidad angular es bien conocida y dada por un simple producto vectorial.
La clave radica, pues, en hacer la conversión entre la velocidad angular relativa al marco de referencia en rotación y el marco de referencia inercial.
Esto se puede lograr a través de lo que son conocidos como los ángulos de Euler, los cuales especifican exactamente cualquier rotación en el espacio.
De esta forma, aunque fuera del alcance de este artículo, se presenta una manera de describir la trayectoria en el espacio de una partícula sobre el objeto.
Es un tema de investigación que se presta a un análisis más riguroso y para el interesado cabe destacar que se presta a la teoría de los cuaterniones de Hamilton.
Bibliografia
| 1. | ↑ | Muller, Derek. n.d. “The Bizarre Behavior of Rotating Bodies, Explained.” https://www.youtube.com/watch?v=1VPfZ_XzisU. |
| 2. | ↑ | Tao, Terrence. n.d. “The ‘Dzhanibekov Effect’ – an Exercise in Mechanics or Fiction? Explain Mathematically a Video from a Space Station.” https://mathoverflow.net/questions/81960/the-dzhanibekov-effect-an-exercise-in-mechanics-or-fiction-explain-mathemat. |
| 3, 5, 6, 8. | ↑ | Taylor, John R. 2005. Classical Mechanics. University Science Books. |
| 4, 7, 13, 14. | ↑ | Vladimir, Arnold, I. 1989. Mathematical Methods of Classical Mechanics Graduate Texts in Mathematics, 60. Graduate Texts in Mathematics. Springer-Verlag, New York. |
| 9. | ↑ | Palaniappan, Vivek. n.d. “Tennis Racket Theorem.” https://medium.com/engineer-quant/tennis-racket-theorem-8fb391098e34. |
| 10, 11. | ↑ | Perko, Lawrence. 2013. Differential Equations and Dynamical Systems. Vol. 7. Texts in Applied Mathematics. Springer. |
| 12. | ↑ | Arnold Vladimir, I. Ordinary Differential Equations. Universitext. Springer-Verlag, 1992 |